Calculating Probability
Perl – Think Again
To tackle mathematical problems with conditional probabilities, math buffs rely on Bayes' formula or discrete distributions, generated by short Perl scripts.
Features
The Monty Hall problem is loved by statisticians around the world [1]. You might be familiar with this puzzle, in which a game show host offers a contestant a choice of three doors – behind one door is a prize, but the other two doors only reveal goats. After the contestant chooses a door, the TV host opens a different door, revealing a goat, and asks the candidate to reconsider (Figure 1). Who would have thought that probabilities in a static television studio could change so dramatically just because the host opens a door without a prize?
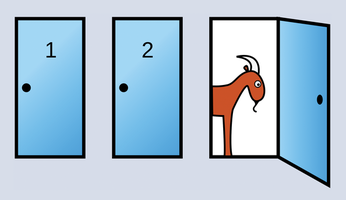Figure 1: Hoping to win the car, the contestant chooses door 1. The host, who knows which door leads to the car, then opens door 3, revealing a goat. He offers the contestant the option of picking another door. Does it make sense for the contestant to change their mind and go for door 2? (Source: Wikipedia)
[...]