Entangled Secrets

Encryption is an everyday part of life on today's Internet. Encryption protocols facilitate virtual private networks (VPNs), protect corporate secrets, and validate banking transactions. Encryption is also the secret sauce behind technologies such as digital signatures and blockchain. The beauty of encryption is that, even if an observer intercepts the transmitted data, the original contents of the message remains hidden from view.

End users and corporations alike have come to depend on encrypted private communication over public networks, but many experts believe the way we think about encryption today will have to change if we want our secrets to stay secret. Cryptographers are looking ahead for a new form of encryption that will meet the needs of the post-quantum era.

The Problem

A quantum computer is a computer that is designed to exploit the mysterious features of quantum mechanics. The basic unit of a conventional computer is binary (0 or 1). A quantum computer, on the other hand, is built around the quantum bit, or qubit, which assumes multiple states simultaneously.

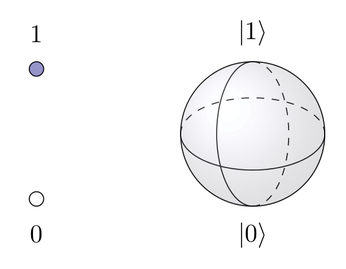
To fully understand the nuances of quantum computing [1], you would need a PhD in physics or computer science (or both), but as a quick illustration, Figure 1 shows a classical bit on the left with two states, zero or one. A qubit (right, represented by a Bloch sphere), can also represent values in between through what is known as superposition, such as a 1 with 65 percent probability and a 0 with 35 percent probability. If you mix up several qubits so that they influence each other, different results can occur, each with a specific probability. This strange but powerful feature lets quantum computers solve certain mathematical problems much more quickly than a conventional computer.

Figure 1: Classical bits (left) versus quantum bits (right).

Quantum computers have been theorized for many years, but the technology is still at the early stages of development. A few test systems exist today, but the kind of large-scale, production-ready quantum computing power necessary to implement the ideas discussed in this article are still a few years away. However, the experts believe the time of the quantum computer will come, and it make sense for the IT industry to prepare.

A quantum computer could theoretically solve any problem you can solve with a conventional computer, but the theorized game-changing efficiency that speeds up solution by orders of magnitude will only work for certain types of problems that can be addressed using specialized quantum algorithms that exploit the power of superposition and qubits.

For example, some popular encryption methods use a key that is a product of prime numbers. The fact that the number 15 is the result of multiplying the two prime factors 3 and 5 is easy to deduce for humans as well as computers, but a number like the one in Listing 1 is difficult for even a computer to reduce to prime factors. The 309-digit number in Listing 1 once carried a US$100,000 prize for anyone who could factor it. The contest ran from 2001 to 2007, and as of the time the contest ended, no one had claimed the prize [2]. Computer scientists have continued to work on the RSA Factoring Challenge numbers even after the contest ended, and to this day, no one has found the prime factors for the number in Listing 1, which is known as RSA-1024.

135066410865995223349603216278805969938881475605667027524485143851526510604859533833940287150571909441798207282164471551373680419703964191743046496589274256239341020864383202110372958725762358509643110564073501508187510676594629205563685529475213500852879416377328533906109750544334999811150056977236890927563

A message properly encrypted with a huge numbers like the one in Listing 1 poses a formidable challenge for a potential eavesdropper working with a conventional computer system. If you know the secret (in this case, the prime factors) the contents is quite trivial to decrypt, but if you don't know the secret, the message is effectively indecipherable.

However, encryption methods based on integer factorization problems of this type are far more vulnerable to attack using a quantum algorithm. According to cryptography experts, Shor's algorithm [3], which was created by the mathematician Peter Shor in 1994, could radically reduce the time needed to factor large numbers.

Other encryption techniques rely on methods that mathematicians refer to with names like the discrete logarithm problem or the elliptic-curve discrete logarithm problem, both of which are also susceptible to attack using quantum techniques.

Symmetric

Symmetric key encryption (where the data is encrypted and decrypted using the same key) is the most efficient means for achieving private communication on the Internet – if you can solve the key distribution problem. Even some procedures that begin with an asymmetric key exchange actually use symmetric encryption for communication and just employ an asymmetric process to communicate the symmetric session key. The most popular symmetric technique in use today is Advanced Encryption Standard (AES).

Symmetric encryption is subject to attack using quantum techniques; however, algorithms such as AES do appear to have some capacity to respond – at least in the near term. The most efficient generic attack by quantum computers on symmetric methods is the Grover algorithm, which was developed by Lov Grover in 1996. The Grover algorithm speeds up mindless brute-force checking of all possible keys. Classically, probability theory says that you have to test half of all possible keys on average. However, even in the worst case, the Grover algorithm requires no more tests than the square root of the number of all possibilities.

The Grover algorithm could thus reduce the bit security by half. In other words, a 128-bit encryption key would provide only the security level of 64-bit encryption in a quantum context. If you double the key length, you get back to the original security level – unattractive, but not technically difficult to implement. In practice, this means that wherever AES-128 is used, for example, you would need to upgrade to AES-256 for equivalent security; or, in the case of hash processes, you would need to upgrade from SHA-256 to SHA-512.

Asymmetric

The security of asymmetric methods, on the other hand, is based on complex mathematical problems such as factoring large numbers or finding discrete logarithms. For sufficiently large numbers, this kind of encryption is practically impossible to solve using classical computers, but quantum computers will have a much better chance. Shor's algorithm provides exponential speed-up for several asymmetric encryption methods on a quantum computer. This speed-up allows the computation of keys of virtually arbitrary length in a meaningful amount of time and makes all widely used asymmetric algorithms, such as RSA, Diffie-Hellman, DSA, and variants based on elliptic curves (ECDH, ECDSA) vulnerable.

The potential obsolescence of the critical asymmetric algorithms that underpin today's Internet economy is one of the reasons why cryptographers are working ahead to ensure that quantum-resilient alternatives are in place before quantum computers emerge from the laboratory.