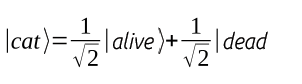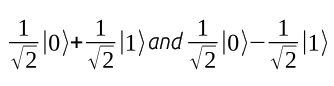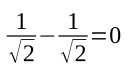An introduction to quantum computing
Cat's Dilemma

The peculiar world of quantum mechanics points the way to a whole new kind of computer. If you're wondering how quantum computers work, we'll give you an inside view.
Quantum computing is a phenomenon that is so close to the edge, it feels like science fiction. The concepts have been around for many years. In 1980, physicist Paul Benioff described a Turing machine built to inhabit the mysterious realm of quantum mechanics. A few years later, Nobel laureate (and American physics icon) Richard Feynman, along with Russian mathematician Yuri Manin, first suggested that a quantum computer could do things that you can't do with an ordinary computer. Mathematicians and computer scientists were intrigued, and since then, they have been busily working ahead on theoretical quantum algorithms for which no suitable hardware yet exists. But the hardware vendors have been busy too, taking on the challenge of designing the quantum logic gates necessary to hold and manipulate entangled photons – at temperatures close to absolute zero. The first 2-qubit experimental quantum computer appeared in 1998, and over the past few years, billions of venture capital dollars have poured into quantum computing startups, while big companies like Google and IBM have built their own teams of quantum physicists to stake a claim on the emerging market.
Working quantum computers exist today, although they are very small scale and experimental, and they still aren't efficient enough to outperform conventional computers. But new breakthroughs occur every year, and many experts believe the age of the quantum computer is not far away. In fact, several vendors offer access to quantum computers via cloud services right now. This article introduces you to some of the principles of quantum computing – and explains why this new technology could have such a powerful effect on our future.
The Basics
The basis of quantum computing is the quantum bit (or qubit), which is both a physical component and a logical unit of information. As you already know, a classic bit can only assume the values 0 or 1. If you access and read a qubit, you also get a value of 0 or 1. Before the reading, however, a fundamentally different situation exists with a quantum bit. Because of a quantum mechanical property known as superposition, additional values between 0 and 1 are possible, leading to computational efficiencies that are not possible with conventional computers.
Before I attempt to describe this strange world of quantum computing, I should add that quantum mechanical phenomena cannot be explained based on experience with our everyday world. A complete explanation would have to start with a description of the double-slit experiment, which you may be familiar with. But since that would offer enough material for a separate article or even a whole book, I will focus instead on how qubits behave and what you can do with them.
This description starts with a model derived from a famous thought experiment: Schrödinger's Cat. In a highly simplified version, imagine that a cat is in a box that isolates the animal from the outside world. A quantum-mechanical event within the box has placed the health status of the animal in limbo (see the box entitled "Schrödinger's Cat" for more information): Whether the cat is alive or dead is indeterminate; a superposition of these two possibilities exists. But this superposition only exists as long as the box remains tightly closed. If I open it, I find either a live or a dead cat. Which of the cases I observe is only decided at the moment of opening, and by chance. There is a probability of 50 percent that the cat is alive, and the same probability that the cat is dead.
Schrödinger's Cat
In the unabridged version of the Schrödinger's cat experiment, the cat is in the box along with an atomic nucleus. The nucleus decays with a certain probability in a certain time. A Geiger counter measures the decay and then releases poison gas that kills the cat. The genius of this thought experiment is that it forces the weird laws of quantum mechanics that typically only occur at the microscopic level to apply to the cat – the cat's state would be indeterminate. In other words, the cat is alive and dead at the same time until the experimenter looks in the box.
Qubits behave in a pretty similar way. An example of a concrete qubit state can look like this 0.6|0> + 0.8|1>. The angle brackets denote the quantum states; this is referred to as Dirac or bra-ket notation [1]. Here |0> or |1> correspond to the classic bit values. They both occur here, |0> with a prefactor of 0.6 (the amplitude) and |1> with an amplitude of 0.8.
The qubit state and the values of the amplitudes themselves cannot be seen. According to the laws of quantum mechanics, there is no method to determine the amplitudes. Quantum mechanical measurement is possible, but it destroys the superposition and returns a random result. To calculate probabilities, I square the amplitudes: I find the qubit to be |0> with probability of 0.36 after the measurement and to be in the |1> state for 64 percent of the time. I can now state the condition of Schrödinger's cat as a superposition:
These square equations might seem a bit unusual. In this example, it is only important for the square of the reciprocal of the square root of 2 to give a value of 1/2. This superposition cannot be detected; it only exists until I open the box and measure it. After that, I would find the cat equally likely to be alive and well, or dead. As long as the box remains tightly closed with no contact with the outside world, the state continues to remain in limbo.
Admittedly, this is just an illustration: Cats are not found in superpositions. In reality, qubits are built with superconductors or ion traps, for example. Superpositions like this are particularly important for computations with qubits:
The values |0> and |1> occur with equal probability here during the measurement. In general, any a|0> + b|1> is a valid superposition, if |a|2 + |b|2 = 1 is true for the amplitudes a and b. There is an infinite number of possible superpositions.
Quantum Parallelism
Now you could rightly ask what makes working with such qubits so desirable, since their properties seem pretty annoying at first glance.
Suppose I have an algorithm that I need to apply to the 256 possible combinations of eight bits. Using a classical computer, I need to run this algorithm 256 times and store the results. What if I use eight qubits instead? The state of an 8-bit quantum register is a superposition of the 256 classical possibilities. If I rework the algorithm to make it quantum-compatible, I can generate a superposition of the 256 results in just one pass. This is known as quantum parallelism. With 100 qubits, a superposition of 2100 function values could be generated in a single run, although existing quantum computers are not yet capable of this.
But I am not done yet. Annoyingly, many representations end here, giving the impression that pretty much any complex problem could be solved with exponential acceleration using a quantum computer. However, the superposition of the 256 or 2100 results cannot be detected. If I measure the register, I see one of these values at random, and I don't even know in advance which one. As the theoretical computer scientist Scott Aaronson has stated, you could instead simply generate one of the 256-bit values in advance with a random generator and then evaluate the function. You wouldn't have to build a quantum computer to do that.
Interference
To find useful quantum algorithms, you need to do more than simply trust in parallelism. You need to ensure that the correct result in the superposition has a higher amplitude (corresponding to a higher probability) and that the amplitude of the incorrect value is very low before the measurement. It is significant that amplitudes can have negative signs. This means that interference can occur: Just as two waves cancel each other out where the peak meets the trough (Figure 1), amplitudes with opposite signs can add up to 0. This possibility for interference does not exist for conventional computers.
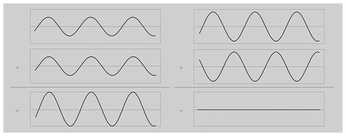 Figure 1: Constructive interference (left) and destructive interference (right). © Reprinted by permission from Springer Nature: Prof. Homeister: Understanding Quantum Computing", 2018
Figure 1: Constructive interference (left) and destructive interference (right). © Reprinted by permission from Springer Nature: Prof. Homeister: Understanding Quantum Computing", 2018
To illustrate this point, imagine you roll two dice and add up the results. There are 36 combinations of two dice, and under fair conditions, each has a probability of 1/36. You are interested in the cases where the result is 10. This can be 4 + 6, 5 + 5 or 6 + 4. The result of 10 has a probability of 1/36 + 1/36 + 1/36 = 1/12. Probabilities always add up in this way, whereas quantum amplitudes can cancel each other out:
At the end of this article, I will describe Grover's search algorithm, in which constructive and destructive interference are used to gradually increase the amplitude of the element being searched for. As you will also learn, quantum algorithms often have a certain probability of error due to the random process involved in measurement.
I did not specify which range of values the amplitudes come from when defining qubit states: They are the complex numbers. While exactly two real numbers have the a magnitude of 1 (1 and -1), there is an infinite number of complex numbers in this property. This expands the interference possibilities.
I'm sure you've heard that quantum computers threaten the security of currently used cryptography methods like RSA. This is due to Shor's algorithm, which can decompose numbers into their prime factors with an exponential speed gain compared with the best-known legacy approach to solving this problem. This acceleration is based on the clever use of interference.
Perhaps by now it has become clear that quantum computers offer an advantage in specific tasks. They complement the familiar legacy computers and open up fundamentally new possibilities, but they do not replace conventional computers.
Buy this article as PDF
(incl. VAT)
Buy Linux Magazine
Subscribe to our Linux Newsletters
Find Linux and Open Source Jobs
Subscribe to our ADMIN Newsletters
Support Our Work
Linux Magazine content is made possible with support from readers like you. Please consider contributing when you’ve found an article to be beneficial.

News
-
Nitrux 6.0 Now Ready to Rock Your World
The latest iteration of the Debian-based distribution includes all kinds of newness.
-
Linux Foundation Reports that Open Source Delivers Better ROI
In a report that may surprise no one in the Linux community, the Linux Foundation found that businesses are finding a 5X return on investment with open source software.
-
Keep Android Open
Google has announced that, soon, anyone looking to develop Android apps will have to first register centrally with Google.
-
Kernel 7.0 Now in Testing
Linus Torvalds has announced the first Release Candidate (RC) for the 7.x kernel is available for those who want to test it.
-
Introducing matrixOS, an Immutable Gentoo-Based Linux Distro
It was only a matter of time before a developer decided one of the most challenging Linux distributions needed to be immutable.
-
Chaos Comes to KDE in KaOS
KaOS devs are making a major change to the distribution, and it all comes down to one system.
-
New Linux Botnet Discovered
The SSHStalker botnet uses IRC C2 to control systems via legacy Linux kernel exploits.
-
The Next Linux Kernel Turns 7.0
Linus Torvalds has announced that after Linux kernel 6.19, we'll finally reach the 7.0 iteration stage.
-
Linux From Scratch Drops SysVinit Support
LFS will no longer support SysVinit.
-
LibreOffice 26.2 Now Available
With new features, improvements, and bug fixes, LibreOffice 26.2 delivers a modern, polished office suite without compromise.