Qiskit – Practical open source framework for quantum computing
IBM is working on increasing the performance of the interaction between hardware and software. The milestones [1] planned for this effort are shown in the IBM Quantum Development Roadmap (Figure 1). To benefit from IBM Quantum hardware, the software and infrastructure must support a wide range of requirements and experiences. This need for versatility requires tools for different types of developers.
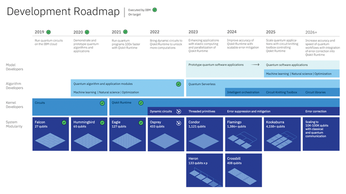Figure 1: IBM has laid out exactly what goals it wants to achieve, and when, in the IBM Quantum Development Roadmap.
Qiskit (think "kiss kit") is a freely available software development kit (SDK) for working with quantum computers at the level of pulses, circuits, or application modules. At least, that's what the SDK home page says. Since its first publication in 2017, the project has grown and undergone some fundamental changes.
[...]
Buy this article as PDF
(incl. VAT)
Buy Linux Magazine
US / Canada
UK / Australia
Subscribe to our Linux Newsletters
Find Linux and Open Source Jobs
Subscribe to our ADMIN Newsletters
Support Our Work
Linux Magazine content is made possible with support from readers like you. Please consider contributing when you’ve found an article to be beneficial.
News
-
Fedora 43 Has Finally Landed
The Fedora Linux developers have announced their latest release, Fedora 43.
-
KDE Unleashes Plasma 6.5
The Plasma 6.5 desktop environment is now available with new features, improvements, and the usual bug fixes.
-
Xubuntu Site Possibly Hacked
It appears that the Xubuntu site was hacked and briefly served up a malicious ZIP file from its download page.
-
LMDE 7 Now Available
Linux Mint Debian Edition, version 7, has been officially released and is based on upstream Debian.
-
Linux Kernel 6.16 Reaches EOL
Linux kernel 6.16 has reached its end of life, which means you'll need to upgrade to the next stable release, Linux kernel 6.17.
-
Amazon Ditches Android for a Linux-Based OS
Amazon has migrated from Android to the Linux-based Vega OS for its Fire TV.
-
Cairo Dock 3.6 Now Available for More Compositors
If you're a fan of third-party desktop docks, then the latest release of Cairo Dock with Wayland support is for you.
-
System76 Unleashes Pop!_OS 24.04 Beta
System76's first beta of Pop!_OS 24.04 is an impressive feat.
-
Linux Kernel 6.17 is Available
Linus Torvalds has announced that the latest kernel has been released with plenty of core improvements and even more hardware support.
-
Kali Linux 2025.3 Released with New Hacking Tools
If you're a Kali Linux fan, you'll be glad to know that the third release of this famous pen-testing distribution is now available with updates for key components.